
NUMERUS
Problematyka przeliczeń współrzędnych
pomiędzy układami "1965" i "2000"
Jak wiadomo od 2010 roku w zastosowaniach geodezyjnych obowiązuje układ współrzędnych "2000", który zastąpił dotychczasowy układ "1965". Nowy układ został już formalnie wprowadzony w większości ośrodków powiatowych, to jednak ciągle, w ten lub inny sposób oraz przy różnych zadaniach praktycznych, wypływa kwestia poprawnego przeliczania współrzędnych z układu "1965"do "2000" lub odwrotnie. Wydaje się, że jeszcze przez długi czas będzie to temat aktualny, zważywszy na zgromadzony zasób geodezyjny, do którego wciąż trzeba sięgać, a który przez dziesięciolecia opracowywany był w układzie "1965".
Poprawne przeliczenie współrzędnych z układu "1965" do układu "2000" (lub odwrotnie) jest zagadnieniem dość złożonym. Po części wynika to z zasadniczych różnic pomiędzy dotychczasowym układem odniesionym do elipsoidy Krasowskiego, a nowym układem odniesionym do elipsoidy GRS80. Ale nie jest słuszne powszechne przekonanie, że różnice układów sprowadzają się do odmienności elipsoid i odwzorowań kartograficznych, bo są to składniki systematyczne i byłyby stosunkowo łatwe do uwzględnienia formułami matematycznymi. Zasadniczą różnicę stanowi odmienność epok technologicznych i wyrównań współrzędnych osnowy I i II klasy, które fizycznie definiują tak jeden, jak i drugi układ.
Są to uwarunkowania merytoryczne, które powodują, że nie jest możliwe jednoznaczne i w pełni precyzyjne transformacyjne przeliczenie współrzędnych z jednego układu na drugi. Każda transformacja może być jedynie mniej lub bardziej satysfakcjonująca, zależnie od przyjętej metody, uwarunkowań lokalnych oraz zastosowanego procesu technologicznego. Natomiast gwarancję uzyskania prawidłowych współrzędnych w nowym układzie daje tylko poprawnie wykonane, ponowne wyrównanie obserwacji
archiwalnych, aczkolwiek nie zawsze jest to możliwe z przyczyn obiektywnych i generalnie jest to metoda droższa. Do ścisłego wyrównania sieci geodezyjnych przydatny może być, dostępny na tej stronie, program UltraNET.
W sytuacji, gdy ponowne wyrównanie nie wchodzi w rachubę pozostaje metoda transformacji. W tym zakresie funkcjonuje w praktyce kilka technologii ale nie wszystkie są równoważne, jeśli chodzi o jakość wyniku finalnego. Niestety można zaobserwować szkodliwe tendencje do upraszczania poprawnego procesu technologicznego, mimo że przecież konsekwencje wadliwie wykonanych przeliczeń są identyczne jak w przypadku błędnego wyznaczenia współrzędnych punktu.
Jasną rzeczą jest to, że stosowana metoda przeliczeń powinna mieć na uwadze również przeznaczenie i akceptowaną dokładność współrzędnych wynikowych. Zapewne do pewnych celów nie ma sensu używać procesu złożonego i pracochłonnego, jeśli nie istnieją wygórowane wymagania dokładnościowe co do współrzędnych finalnych. Powinna to jednak być decyzja świadoma, a nie wynikająca z niewiedzy, lenistwa lub braku kunsztu geodezyjnego.
W pozostałych przypadkach nie powinny być stosowane uproszczenia, i nie ma tu znaczenia czy powodują one błędność wyniku o 2cm, czy też o 20 cm. Geodezja akceptuje bowiem różnego rodzaju błędy przypadkowe, ale nie toleruje błędów systematycznych, których istnienie zawsze powinno być interpretowane jako usterka jakościowa.
Pełny, merytorycznie poprawny proces technologiczny związany z przeliczeniem współrzędnych pomiędzy układami "1965" i "2000" normuje instrukcja techniczna G-2 z 2001 r. pt. "Szczegółowa pozioma i wysokościowa osnowa geodezyjna i przeliczenia współrzędnych między układami". Jest to procedura obliczeniowa zgodna ze sztuką geodezyjną, warto więc stosować się do zawartych tam zaleceń.
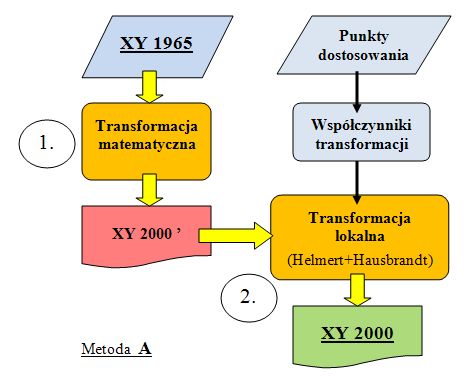
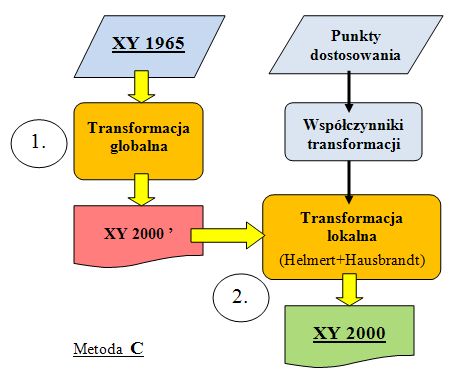
Całość zalecanego procesu dla przeliczeń w kierunku 1965 -> 2000 można zilustrować w postaci schematu blokowego przedstawionego obok. Składa się on z dwóch obligatoryjnych etapów następujących kolejno po sobie:
Etap 1. Doprowadzenie współrzędnych z układu pierwotnego do płaszczyzny matematycznej tożsamej z układem wtórnym. Jest to konwersja matematyczna oparta na znanych parametrach transformacji 3D wynikających z przesunięcia i obrotu osi elipsoid odniesienia obu układów, szczegółowo zdefiniowana w Wytycznych Technicznych G-1.10 z 2001 r. pt. "Formuły odwzorowawcze i parametry układów współrzędnych".
Etap 2. Transformacja lokalna metodą Helmerta z wykorzystaniem współczynników transformacji określonych na podstawie punktów dostosowania wyższej klasy. Bardzo ważnym elementem tego etapu jest też finalna korekta posttransformacyjna metodą Hausbrandt'a, której zadaniem jest wyzerowanie odchyłek na punktach dostosowania transformacji.
Zrealizowanie powyższej procedury obliczeniowej zapewnia dobrą zgodność przeliczonych współrzędnych na poziomie wartości empirycznych (katalogowych) i geometryczną spójność z osnową wyższej klasy, co powinno być cechą każdej dobrej konwersji współrzędnych.
Współrzędne uzyskane po zrealizowaniu pierwszego etapu obliczeń posiadają dość słabą jakość. Różnice współrzędnych na punktach geodezyjnej osnowy państwowej, w zależności od lokalizacji punktu, mogą osięgać nawet wartości rzędu decymetrów, na skutek rzeczywistych deformacji układu "1965" w stosunku do układu "2000". Tak więc użycie drugiego etapu obliczeń jest tu bezsporne w większości zastosowań praktycznych.
Jako swojego rodzaju alternatywa dla transformacji 3D został opracowany i spopularyzowany przez profesora R.Kadaja algorytm nazywany "metodą korekt globalnych układu "1965" lub krócej "metodą transformacji globalnej".
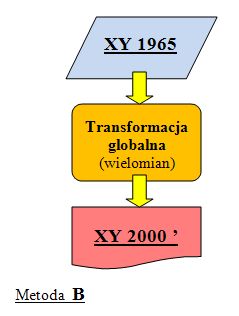
Jest to aparat matematyczny oparty na funkcji wielomianowej wyższego stopnia, przy czym do wyznaczenia parametrów wielomianu wykorzystano punkty łączne osnowy I i II klasy. Metoda pozwala na lepsze zbliżenie się do współrzędnych empirycznych niż posłużenie się wyżej wspomnianą transformacją 3D. W uzasadnionych przypadkach metoda może być przydatna jako samodzielny proces obliczeniowy ale w zastosowaniach o niskich wymogach dokładnościowych albowiem nie likwiduje do końca lokalnych dystorsji współrzędnych. Mimo to "goła" transformacja globalna niestety zaczęła być postrzegana przez wielu praktyków jako samodzielna technologia przeliczeń, zamiennik dla pełnego procesu technologicznego związanego z konwersją współrzędnych. Poprawa jakości współrzędnych po pierwszym etapie obliczeń powoduje pokusę zrezygnowania z finalnej transformacji lokalnej, co uwalnia od niekiedy uciążliwych czynności z nią związanych. Tak więc wykonawca, który świadomie lub nieświadomie decydyje się na takie uproszczenie prac musi wkalkulować, że odbywa się to kosztem jakości współrzędnych finalnych. Z perspektywy wykonawcy obliczeń atrakcyjne jest to, że do konwersji współrzędnych metodą korekt globalnych wystarczy tylko posiadanie odpowiedniej aplikacji komputerowej, natomiast do prawidłowego ich zakończenia z użyciem transformacji lokalnej konieczne było by pozyskanie z PZGiK punktów łącznych wyższej klasy, wykonanie ich prawidłowego doboru oraz przeprowadzenie analizy ich wzajemnej spójności, co jest trudniejsze i bardziej złożone w realizacji, wymaga też odpowiedniego doświadczenia fachowego.
Metoda nie zapewnia idealnego wpasowania we współrzędne empiryczne na całym obszarze. Żeby tak było, wielomian musiałby mieć dla każdej współrzędnej tyle współczynników ile jest punktów I i II klasy na obszarze strefy układu "1965", czyli kilkanaście tysięcy, co jest oczywiście nieosiągalne. Ze względu na ograniczenia modelowe omawiane funkcje cechuje więc pewien stopień generalizacji, na co nie bez powodu wskazuje też sama ich nazwa - korekty "globalne". Spełniają one warunek najlepszego dopasowania układów współrzędnych na dużym obszarze (strefy układu "1965"), natomiast nie ujmują precyzyjnie wszystkich deformacji lokalnych, gdzie mogą być, i często są, różnego rodzaju lokalne anomalie współrzędnych. Sprawdza się więc znane zjawisko, że to co jest dobre dla dużego obszaru pod względem średniej wartości jakiegoś kryterium, może mieć sporo "odskoków" na plus i minus w konkretnych miejscach. Sytuacja jest więc trochę podobna jak jest z elipsoidą WGS84 - wiadomo, że aproksymuje ona najlepiej powierzchnię całej Ziemi ale w przypadku konkretnego obszaru wynik może być mało rewelacyjny, czego przykładem jest Polska, gdzie różnice wysokości normalnej i elipsoidalnej wynoszą aż 30-40 m.
Warto też zauważyć, że metoda nie uwzględnia dystrybucji poprawek Hausbrandt'a z punktów osnowy użytych do określenia parametrów wielomianu.
Istotną przeszkodą w poprawnym wykorzystaniu metody korekt globalnych jest brak informacji o jej gwarantowanej dokładności oraz brak specyfikacji, w których typowych zadaniach geodezyjnych może ona być użyta jako proces samodzielny, a gdzie powinna być zakończona transformacją lokalną. Wykonawca podejmuje więc po omacku decyzję o wyborze technologii przeliczeń, co powoduje niebezpieczeństwo, że może to być wybór, który nie spełnia kryteriów dokładnościowych jakie odpowiadają celowi prac. Błąd średni korekt globalnych jest podawany jako wartość 0.03 - 0.04 m, natomiast niestety nigdzie nie znalazłem informacji jakiego rzędu były odchyłki maksymalne na punktach łącznych przyjętych do wyliczenia współczynników wielomianu oraz jaki był ich rozkład powierzchniowy. Mogłoby to być bardzo przydatne przy ocenie dokładności i przydatności metody w konkretnych rejonach kraju. Faktyczna dokładność przeliczenia współrzędnych punktu będzie bowiem raczej bliska odchyłkom na pobliskich punktach łącznych, niż błędowi średniemu transformacji z całej strefy układu "1965", który jest przecież tylko pewną charakterystyką statystyczną.
Doświadczenia praktyczne wskazują, że dokładność metody zależy od rejonu kraju. Na wielu obszarach uzyskiwana jest dokładność rzędu kilku centymetrów. Można jednak również spotkać miejsca, gdzie rozbieżności w stosunku do współrzędnych katalogowych osnowy I i II klasy uzyskanych metodą ścisłą, są dużo większe. Swojego czasu trafiło mi się na przykład zadanie na obszarze I-szej strefy układu "1965" pokazanym niżej, gdzie zlokalizowane jest ok. 20 punktów I i II klasy.
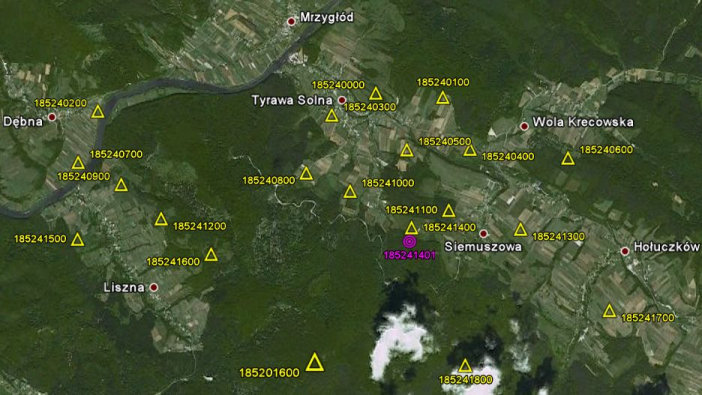
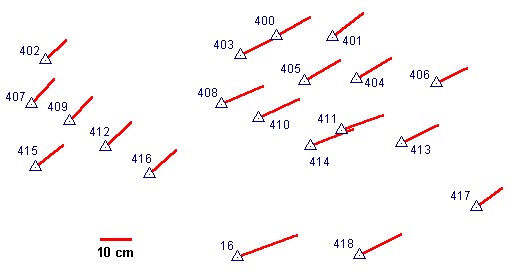
Ponieważ dysponowałem współrzędnymi katalogowymi tych punktów w układach "1965" i "2000", interesujące było zbadanie na ile wynik przeliczenia współrzędnych metodą korekt układu "1965" zgadza się z wartościami katalogowymi. Okazało się, że jest to zgodność bardzo słaba - przeciętna różnica wektorowa wynosi tu 0.14 m, a różnica maksymalna to 0.22 m.
Co gorsza, wszystkie wektory różnic mają bardzo podobny kierunek i zwrot, a więc nie jest to kwestia błędu współrzędnych jakiegoś indywidualnego punktu, tylko wyraźne skażenie systematyczne obejmujące dość rozległy obszar.
Gdyby w tym rejonie kraju ktoś zechciał użyć do przeliczeń metody korekt układu "1965" bez odpowiedniej transformacji lokalnej to jakość uzyskanych współrzędnych dalece odbiegałaby od deklarowanego błędu średniego tej metody 0.03-0.04 m.
Ciekawe może być również zbadanie na ile korekty układu "1965" zapewniają tożsamość przeliczeń w obszarach styku sąsiednich stref układu "1965". Jest to istotne w przypadku jednostek administracyjnych usytuowanych na stykających się fragmentach dwóch stref układu "1965" lub obiektów liniowych (np. tras komunikacyjnych) przecinających granice dwóch stref, gdzie w celu zapewnienia jednorodności współrzędnych zastosowano ekstrapolację współrzędnych z jednej strefy na obszar sąsiedniej strefy układu "1965". Intuicyjnie czujemy, że w takim przypadku w układzie "2000" powinna zachodzić spójność współrzędnych pomiędzy sąsiednimi punktami niezależnie od tego z jakiej strefy układu "1965" pochodzą współrzędne pierwotne.
Aby to sprawdzić obrałem punkt w rejonie styku III i IV strefy układu "1965". W odległości ok. 1 km od punktu zlokalizowane są punkty osnowy państwowej o numerach 375220500 (ze strefy III) oraz 425101000 (ze strefy IV).
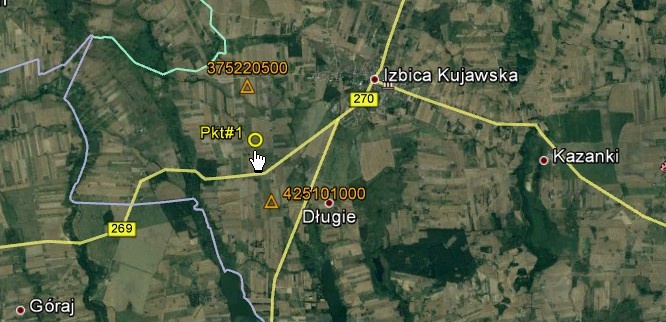
Współrzędne wybranego punktu określono w III strefie układu "1965" i przeliczono również na matematycznie tożsame wartości w strefie IV zgodnie ze ścisłymi formułami odwzorowania "1965".
Następnie w ramach każdej pary współrzędnych (odrębnie w każdej strefie układu "1965") przeprowadzano konwersję współrzędnych do układu "2000" z wykorzystaniem funkcji korekt globalnych stosownej strefy układu "1965". Szczegóły obliczeń przedstawiono w tabelce niżej.
| Strefa układu "1965" | Współrzędne źródłowe w układzie "1965" | Przeliczone współrzędne w układzie "2000/18" | ||
|---|---|---|---|---|
| X | Y | X | Y | |
| Strefa III | 5869940.94 | 3618256.01 | 5808823.51 | 6549664.33 |
| Strafa IV | 5711306.38 | 3843111.98 | 5808823.56 | 6549664.35 |
| Różnice współrzędnych w ukł. "2000" | 0.05 | 0.02 | ||
Dwukrotnie przeliczano punkt identyczny matematycznie więc zasadne było oczekiwać, że po stronie układu "2000" uzyskamy identyczne współrzędne niezależnie od tego, z której strefy układu "1965" pochodzą współrzędne źródłowe. W wyniku porównania uzyskujemy niestety po stronie układu "2000" różnicę wektorową współrzędnych ponad 0.05 m.
Oznacza to, że funkcje korekt układu "1965" niezbyt dokładnie zabezpieczają spójność współrzędnych sąsiednich punktów pochodzących z różnych stref układu "1965".
Jak widać z powyższych doświadczeń potwierdza się przekonanie, że transformacja globalna użyta jako samodzielny proces nie jest dostatecznie dobrą metodą przeliczeń. Generalnie same korekty globalne, bez uzupełniającego szlifu, to tylko półprodukt numeryczny. No chyba, że nie zależy nam na najwyższej jakości i godzimy się na mniejszy lub większy błąd systematyczny.
Poprawne wyniki możemy uzyskać dopiero, jeśli po korektach globalnych zastosujemy transformację lokalną w oparciu o odpowiednio dobrane punkty dostosowania oraz rozrzucenie odchyłek metodą Hausbrandt'a.
Powstaje więc dwuetapowa procedura numeryczna całkiem podobna do metody przedstawionej na schemacie A. Obie metody różnią się tylko aparatem matematycznym przy pomocy, którego jest realizowany etap 1 procesu technologicznego.
Tak więc metoda korekt układu "1965" i transformacja lokalna nie wykluczają się lecz wzajemnie się uzupełniają. Oba rodzaje transformacji zastosowane łącznie jedna po drugiej przyczyniają się do znacznego poprawienia wyniku przeliczeń.
Zwolennicy metody samodzielnej korekty globalnej, chętnie używają argumentu, że umożliwia to "naprawienie" anomalii układu "1965". Wydaje się, że przywoływanie takiego argumentu w zastosowaniach praktycznych nie jest słuszne. Naprawa układu mogłoby być ciekawym zagadnieniem teoretycznym, a nie w przypadku konkretnego zadania produkcyjnego. Przeliczenie realizowane pod konkretny cel nie powinno naprawiać układu tylko możliwie najlepiej wpasować jeden układ w drugi, biorąc pod uwagę, że nie są to dwie abstrakcyjne płaszczyzny lecz zdefiniowane matematycznie punkty w terenie. Tymi punktami jest osnowa geodezyjna z konkretnymi wartościami współrzędnych katalogowych oraz odniesione do nich tony pochodnych materiałów geodezyjnych zgromadzonych przez lata w zasobie geodezyjnym. Tu nie da się niczego naprawić. Jeśli gdzieś była anomalia to teraz właśnie trzeba się do niej dopasować. W przeciwnym wypadku wyniki przeliczenia nie będą spójne z zasobem geodezyjnym, a przeliczone stare pomiary rozjadą się z pomiarem nowym. Gdyby na obszarze omawianym wyżej geodeta chciał przy okazji przeliczenia "naprawiać" układ "1965", to najbardziej ewidentnym wynikiem tych działań byłoby rozjechanie się przeliczonych punktów (np. granic działek) o kilkanaście centymetrów w stosunku do nowego pomiaru zrealizowanego metodą GPS. A nie o to chodzi.
Powstaje jeszcze pytanie, czy któryś z wyżej omawianych procesów przeliczeniowych, A lub C, jest lepszy od drugiego?
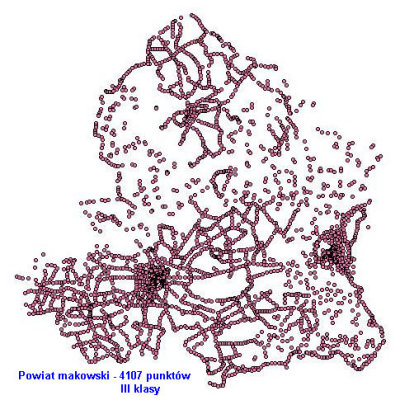
Eksperymenty przeprowadzone na wielu konkretnych obiektach produkcyjnych (m.in. takich jak pokazane obok) wskazują, że na obszarze wielkości przeciętnego powiatu obie metody są całkowicie równoważne. Jak dotąd nie udało mi się zauważyć różnicy między nimi większej niż 0.001 - 0.003 m w wartościach współrzędnych finalnych. Oczywiście przy założeniu, że w obu metodach identyczny jest zestaw punktów łącznych transformacji lokalnej.
Zauważalna jest tylko różnica w wartości oszacowania błędu średniego transformacji mt. Dla metody C po finalnej transformacji lokalnej otrzymuje się zwykle mniejsze wartości mt. Jest to zrozumiałe, ponieważ wielomian zaangażowany w pierwszym etapie procesu bierze na siebie część różnic systematycznych pomiędzy układem pierwotnym i wtórnym. W związku z tym na etapie transformacji lokalnej pozostają mniejsze odchyłki na punktach dostosowania, co powoduje jakby bardziej optymistyczną ocenę dokładności mt.
Gdyby dla metody C obliczyć błąd sumaryczny z procesów (1)+(2) według prawa przenoszenia się błędów średnich, to zapewne i pod tym względem dla obu metod wynik byłby podobny.
W programie GeoKonwerter istnieje bardzo prosty sposób, żeby przetestować praktycznie różnicę pomiędzy metodą A i C dla konkretnego obiektu, ponieważ istnieje możliwość wyboru realizowanej metody.

Jeśli chodzi o stopień złożoności numerycznej, to obie metody różnią się dość zasadniczo w zakresie pierwszego etapu obliczeń, ale z punktu widzenia wykonawcy nie ma sensu tego rozpatrywać, ponieważ w obu przypadkach wszystko wykonuje odpowiedni program komputerowy. Dla wykonawcy obliczeń jest to więc różnica niezauważalna.
Na koniec należy podkreślić bardzo ważne znaczenie punktów dostosowania transformacji lokalnej. Mają one decydujący wpływ na wynik przeliczenia, więc ich ewentualny błędny dobór spowoduje wadliwość finalnych współrzędnych zarówno w metodzie A, jak i w metodzie C. Warto więc poświęcić specjalną uwagę doborowi tych punktów, tym bardziej, że na przykład w programie GeoKonwerter jest to czynność jednorazowa. Program ma tę zaletę, że punktami łącznymi transformacji zajmujemy się tylko jeden raz - na etapie obliczania współczynników dla rejonu opracowania lub całego powiatu. Potem interesują nas tylko bieżące pliki masówki transformacyjnej. Te same współczynniki mogą być używane wielokrotnie do przeliczeń różnych plików, a istnieje przy tym gwarancja, że wszystkie przeliczenia są wzajemnie spójne, niezależnie od tego kiedy i przez kogo zostały wykonane.
Opracowanie:
Wiesław Kozakiewicz
www.numerus.net.pl

Copyright© NUMERUS Wiesław Kozakiewicz www.numerus.net.pl
