Testy programu UltraNet

NUMERUS

Testy praktyczne programu UltraNET

W katalogu instalacji programu w podkatalogu Dane testowe umieszczono dane wejściowe dla kilku obiektów obliczonych programem UltraNet. Dane te można wykorzystać do przetestowania funkcji obliczeniowych programu oraz sposobu jego obsługi jak również sposobu kodowania danych.

Przykład nr 1 - Wyrównanie sieci wektorowej GNSS - wyrównanie 3D

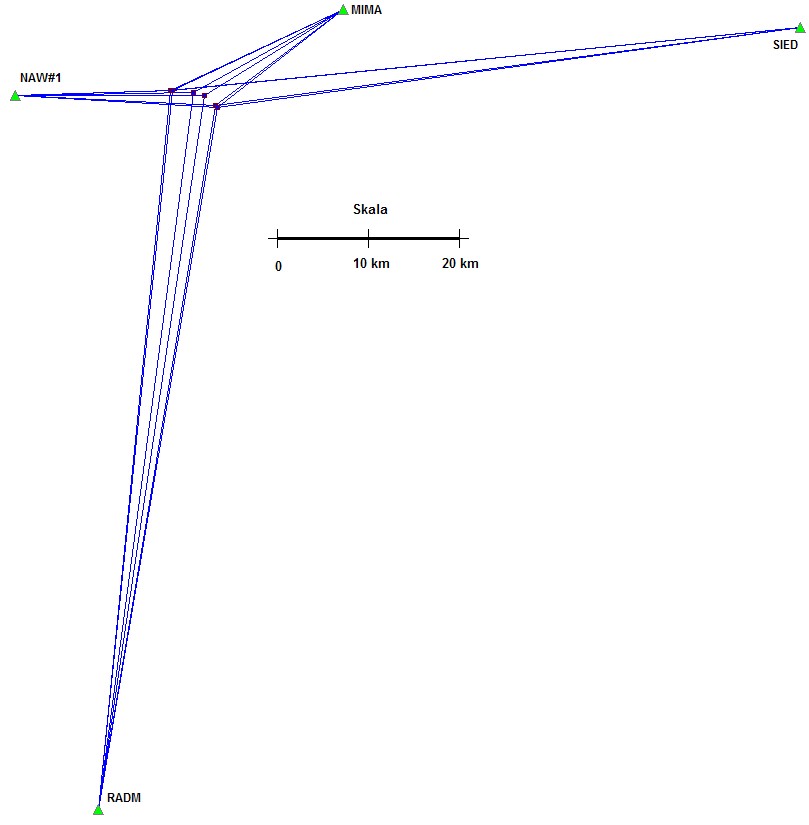
Testowa sieć była pomierzona metodą statyczną GNSS, jest stosunkowo mała ale zawiera wszystkie niezbędne parametry nawiązania konieczne dla obiektu tego rodzaju. Posiada nawiązanie poziome na 4 punkty wyższego rzędu oraz nawiązanie wysokościowe również na 4 punkty. Większość punktów nawiązania wysokościowego nie pokrywa się z punktami nawiązania poziomego, czyli tak jak najczęściej bywa w praktyce przy zakładaniu osnowy szczegółowej. Do nawiązania poziomego włączone są odległe stacje ASG-EUPOS, co obecnie również jest sytuacją typowa w większości sieci geodezyjnych realizowanych techniką GNSS. W pliku STALE3D.txt współrzędne punktów nawiązania celowo podano w niejednolitym typie (jak XYZ, BL, XY i H_elips), co ilustruje elastyczność i uniwersalność programu pod tym względem. Konstrukcję sieci przedstawia rysunek niżej.

W celu zrealizowania wyrównania należy wskazać w programie ścieżkę do danych obiektu, wybrać opcję obliczeń SIEĆ 3D a następnie wcisnąć przycisk Wykonaj wyrównanie sieci wektorowej.

Zobacz raport wyrównania - Wyrównanie3D

Przyklad nr 2 - Wyrównanie poziome sieci hybrydowej - wyrównanie 3D + 2D

Do testu celowo wybrano sieć hybrydową złożoną z obserwacji GNSS wykonanych metodą statyczną oraz klasycznych obserwacji kątowo-liniowych.
Podsieć GNSS stanowi konstrukcja omówiona w przykładzie nr 1. Pomiędzy punktami GNSS (niebieskie) założono 17 punktów wyznaczonych metodą klasyczną (zielone), tak jak pokazuje to poniższy rysunek.

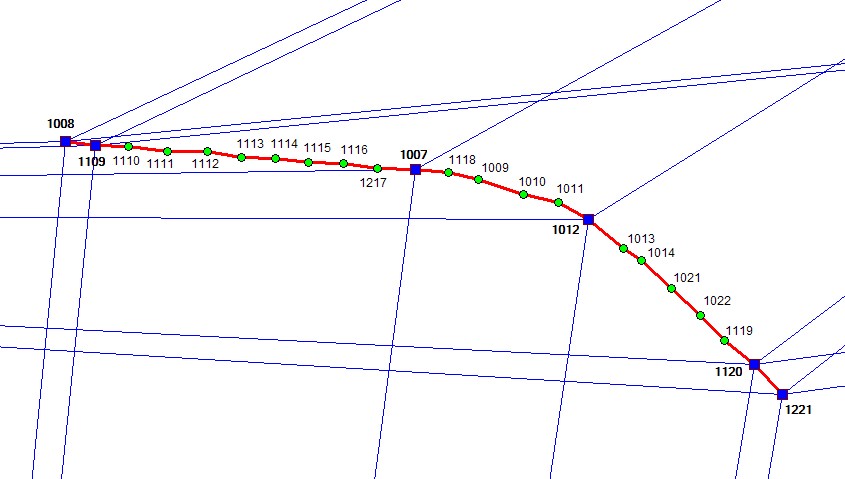
Łączne wyrównanie dla takiej poziomej sieci hybrydowej wykonuje się jako wyrównanie 2D na płaszczyźnie odwzorowawczej układu PL-2000. Test pozwala zaobserwować jak przy pomocy programu UltraNET można dokonać poprawnego wyrównania obiektu, który technologicznie jest nieco bardziej skomplikowanym przypadkiem sieci.

Opracowanie numeryczne realizujemy w dwóch krokach, załączony przykład zawiera dane do obu etapów:

Etap 1
Jest to niezbędny etap wstępny, gdzie wyrównaniu podlegają wyłącznie obserwacje GNSS. W tym celu wybieramy w programie opcję SIEĆ 3D i możemy wykonać obliczenia dokładnie tak jak w przykładzie nr 1. Jednakże zamiast wyrównania z przymusem nawiązania możemy tu wykonać wyrównanie pseudoswobodne w nawiązaniu na jeden punkt, którego zadaniem będzie umiejscowienie wektorów w trójwymiarowej przestrzeni układu geocentrycznego XYZ. Takie umiejscowienie jest niezbędne do prawidłowego zrzutowania wektorów na elipsoidę odniesienia, czyli policzenia tzw. pseudoobserwacji GNSS.
Warto zauważyć, że w wyniku tej operacji, po wyrównaniu program utworzy dwa pliki potrzebne do następnego etapu - są to:
ObsGPS.txt - plik pseudoobserwacji GNSS,
XYh3D.txt - plik współrzędnych dla punktów GNSS, które w następnym etapie będą traktowane jak współrzędne przybliżone tych punktów.

Etap 2
To będzie finalne, łączne wyrównanie całej sieci.
Do wyrównania potrzebny będzie plik wspłórzędnych nawiązania sieci, który tworzymy na wstępie w edytorze zewnętrznym. Umieszczamy w nim punkty, które były w pliku STALE3D.txt i nadajemy mu nazwę STALE2D.txt.
Następnie wybieramy w programie opcję SIEĆ 2D i tu wciskamy kolejno dwa przyciski
- klawisz Oblicz współrzędne przybliżone, co spowoduje obliczenie współrzędnych przybliżonych na poligonowych ciągach kątowo-liniowych,
- klawisz Wykonaj wyrównanie sieci poziomej.

Zobacz raport wyrównania - Wyrównanie2D

Przykład nr 3 - Wyrównanie poziome sieci hybrydowej - wyrównanie 3D + 2D

Podobnie jak w przykładzie nr 2, tu również zadaniem jest wyrównanie sieci hybrydowej ale dla odmiany obserwacje GNSS wykonano tu metodą RTN. Jest to przykład małego obiektu, gdzie wyznaczono dwie pary punktów metodą RTN, a pomiędzy nimi założono ciąg klasyczny złożony z kliku punktów. Jest to typowa sytuacja poprowadzenia ciągu osnowy pomiarowej przez teren zalesiony, gdy na skrajach tego terenu istnieją dobre warunki GNSS. Naszym zadaniem będzie łączne wyrównanie wszystkich obserwacji jako sieć jednorzędowa.

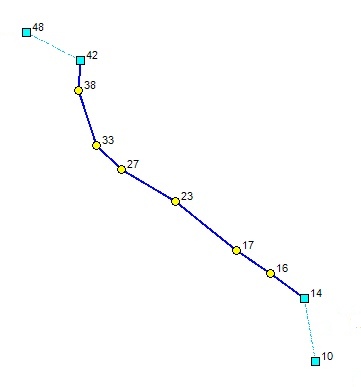
Podobnie jak w przykładzie nr 2 opracowanie numeryczne realizujemy tu w dwóch krokach, załączony przykład zawiera dane do obu etapów:

Etap 1
Jest to wstępne wyrównanie samych obserwacji GNSS. Trzeba tylko zauważyć, że każda skrajna para punktów GNSS została pomierzona z dwóch niezależnych inicjalizacji odbiornika. Plik wektorów został utworzony na podstawie raportu pomiaru RTN jako wykaz przyrostów DX,DY,DZ od stacji bazowych VRS do punktów wyznaczanych.
Nawiązaniem sieci będą stacje bazowe VRS pomiaru RTN, tak więc w pliku współrzędnych punktów nawiązania umieszczono współrzędne stacji bazowych RTN w układzie geocentrycznym X,Y,Z - wartości również pobrane z raportu pomiaru RTN. Jeżeli dysponujemy plikiem odbiornikowym RW5 to potrzebny plik wektorów od stacji bazowych do punktów masówki obserwacyjnej oraz współrzędne tychże stacji bazowych możemy utworzyć (wyeksportować z RW5) za pomocą funkcji pomocniczej programu znajdującej się w zakładce Dodatki.
W efekcie wyrównujemu podsieć GNSS jak na rysunku niżej

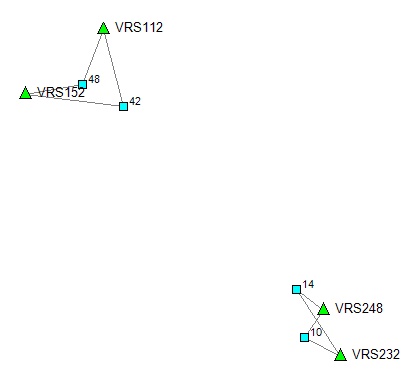
Wybieramy w programie opcję SIEĆ 3D i wykonujemy wyrównanie obserwacji GNSS. Warto zauważyć, że w wyniku tej operacji, po wyrównaniu program utworzy dwa pliki potrzebne do następnego etapu - są to:
ObsGPS.txt - plik pseudoobserwacji GNSS,
XYh3D.txt - plik współrzędnych dla punktów GNSS, które w następnym etapie będą traktowane jak współrzędne przybliżone tych punktów.

Etap 2
To będzie finalne, łączne wyrównanie całej sieci.
Do wyrównania potrzebny będzie plik współrzędnych nawiązania sieci, który tworzymy na wstępie w edytorze zewnętrznym. Umieszczamy w nim punkty, które były w pliku STALE3D.txt i nadajemy mu nazwę STALE2D.txt.
Następnie wybieramy w programie opcję SIEĆ 2D i tu wciskamy kolejno dwa przyciski
- klawisz Oblicz współrzędne przybliżone, co spowoduje obliczenie współrzędnych przybliżonych na ciągu kątowo-liniowym,
- klawisz Wykonaj wyrównanie sieci poziomej.

W efekcie wyrównamy sieci hybrydową, którą przedstawia rysunek niżej

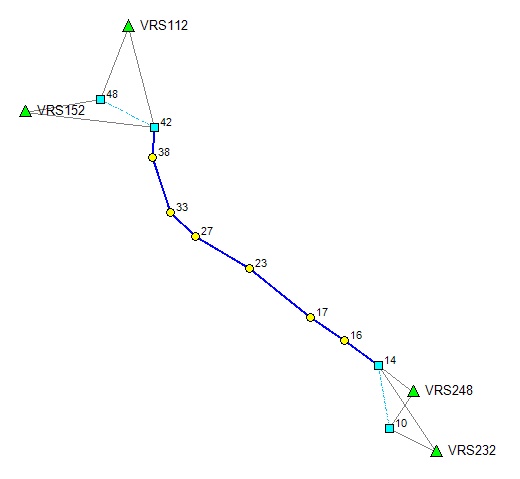
Zobacz raport wyrównania - Wyrównanie2D

Przykład nr 4 - Wyrównanie poziome sieci kątowo-liniowej - wyrównanie 2D

Jako przykład wyrównania sieci stricte kątow--liniowej podano tu siatkę archiwalnej osnowy ewidencyjnej, która była rewitalizowana w układzie PL-2000. W pliku STALE2D.txt znajduje się kilka punktów nawiazania, dla których założono bezbłędność współrzędnych. Jest tu również kilka punktów, dla których przyjęto błędność współrzędnych mp=0.05 m. Szkic sieci prezentuje poniższy rysunek

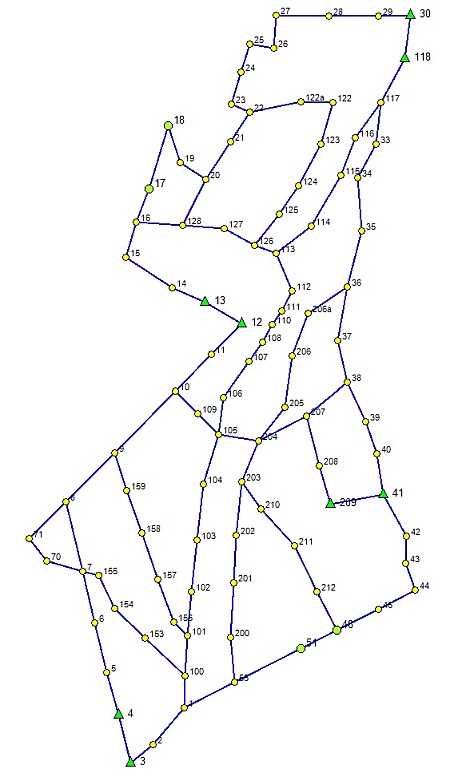
Dane testowe zawierają wszystkie pliki wejściowe - obserwacje i punkty nawiązania sieci. W celu wykonania obliczeń wystarczy wskazać ścieżkę dojścia do obiektu i wybrać opcję SIEĆ 2D. Następnie wykonać kolejno następujące operacje (wcisnąć przyciski):
- Oblicz współrzędne przybliżone,
- Wykonaj wyrównanie ...

Zobacz raport wyrównania - Wyrównanie2D

Przykład nr 5 - Wyrównanie wysokościowe sieci niwelacyjnej - wyrównanie 1D

To przykład typowej wielowęzłowej sieci niwelacyjnej, której konstrukcję tworzą odcinki pomierzone metodą niwelacji geometrycznej. Nawiązanie sieci tworzą repery wyższego rzędu (na rysunku kolor niebieski) traktowane jako bezbłędne. Do wagowania obserwacji, stosownie do zasad niwelacji geometrycznej, posłużyły długości odcinków niwelacji.

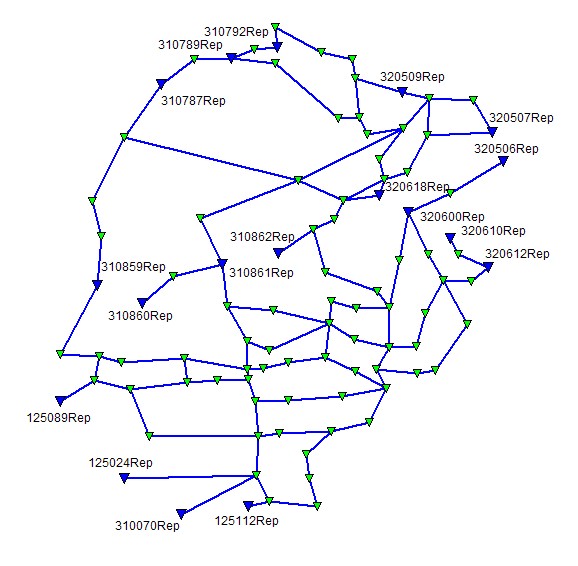
Dane testowe zawierają wszystkie pliki wejściowe - obserwacje i punkty nawiązania sieci. W celu wykonania obliczeń wystarczy wskazać ścieżkę dojścia do obiektu, wybrać opcję SIEĆ 1D i wcisnąć przyciski Wykonaj wyrównanie

Wyrównanie zostaje zrealizowane po wciśnięciu przycisku Wykonaj wyrównanie. Wcześniej należy zadeklarować na panelu programu błędy a'priori dla obserwacji co jest potrzebne do właściwego zwagowania sieci.

Zobacz raport wyrównania - Wyrównanie1D

Przykład nr 6 - Wyrównanie niwelacji satelitarnej - wyrównanie 1D

Zadaniem jest tu wyrównanie wysokościowej sieci hybrydowej, której konstrukcję tworzą odcinki niwelacji satelitarnej oraz odcinki niwelacji geometrycznej. Wektory satelitarne zostały pomierzone metodą statyczną GNSS, obliczone w wyniku postprocessingu.

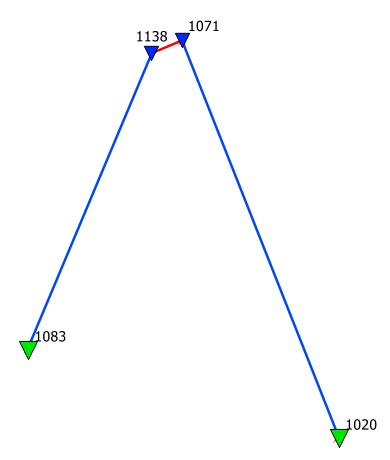
Szkic sieci przedstawia rysunek obok.
Wyznaczane są tu 2 nowe repery osnowy wysokościowej o numerach 1071 i 1138. Sieć jest nawiązana na 2 repery osnowy wyższej klasy o numerach 1020 i 1083.
Metodą niwelacji satelitarnej zostały pomierzone 2 dłuższe odcinki pokazane kolorem niebieskim o długości 4-5 km. Jeden krótki odcinek (pomiędzy reperami wyznaczanymi) został pomierzony za pomocą klasycznej niwelacji geometrycznej (kolor czerwony). Odcinek pomierzony klasycznie stanowi jednocześnie dobrą kontrolę, ponieważ zamyka linię niwelacyjną - ewentualny błąd na którymś z pokazanych odcinków niwelacji musi objawić się w wyrównaniu dużymi poprawkami do obserwacji. Można by go oczywiście też pomierzyć satelitarnie. Uzyskano by potrzebne zamknięcie linii niwelacyjnej ale bez kontroli zadania poprzez niezależne przewyższenie geometryczne.
Ważną okolicznością jest to, że wyznaczany reper 1071 oraz reper nawiązania 1083 to repery ścienne, a więc takie których nie można stacjonować odbiornikiem GNSS. W związku z tym w ich pobliżu założono ekscentry 1071ex i 1083ex posiadające dobre warunki GNSS. Pomiary GNSS wykonano właśnie na wspomnianych ekscentrach. Natomiast jednym stanowiskiem niwelatora określono różnicę wysokości pomiędzy reperem i jego ekscentrem i te przewyższenia będą również uczestniczyć w finalnym wyrównaniu sieci.

Tak wiec sytuacja konstrukcyjna, powiedzmy na punkcie 1071 wygląda jak na rysunku niżej

W celu pomiaru wektorów wykonano dwie sesje obserwacyjne metodą statyczną z użyciem 3 odbiorników GPS. Za każdym razem 2 odbiorniki stacjonowały punkty sieci natomiast trzeci odbiornik zabezpieczał nawiązanie na punkt nr 9000 o znanych współrzędnych i wysokości. Funkcją tego punktu było właściwe zlokalizowanie pomiarów w przestrzeni XYZ, co jest potrzebne do właściwej konwersji wektorów na przewyższenia.
Na pierwszym rysunku pokazano najistotniejsze odcinki niwelacji sateltarnej, które przyjęto do obliczeń. Nie ma oczywiście przeszkód, żeby dodawać do obliczeń również dodatkowe wektory jakie mogą powstać w przypadku, gdy sesje pomiarowe są realizowane przez kilka odbiorników.
Opracowanie numeryczne takiego zadania realizujemy w dwóch krokach, załączony przykład zawiera dane do obu etapów:

Etap 1
Jest to niezbędny etap wstępny, gdzie jakby wyrównaniu podlegają wyłącznie obserwacje GNSS. W tym celu wybieramy w programie opcję SIEĆ 3D i możemy wykonać obliczenia.

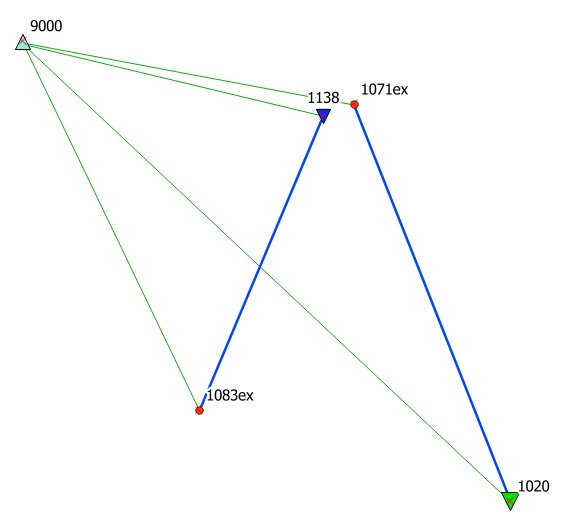
Wykonujemy tu wyrównanie pseudoswobodne w związku z tym jako punkt stały zostaje użyty wyżej wspomniany punkt 9000. Pozostałe punkty uzyskują współrzędne poprzez propagację dzięci temu wszystkie wektory zostają umiejscowione w geocentrycznym układzie XYZ.
Do wyrównania wchodzą dwa pliki: Wektory.txt oraz Stale3D.txt.
Najważniejszym efektem tego etapu obliczeń jest to, że po wyrównaniu program utworzy tu plik pn. DhGPS.txt, który zawiera przewyższenia odpowiadające pomierzonym wektorom. Istotne jest to, że są to przewyższenia normalne, a nie przewyższenia elipsoidalne. Tylko przewyższenia normalne są spójne co do ich rodzaju z przewyższeniami pochodzącymi z niwelacji geometrycznej, dzięki temu te dwa typy obserwacji będą mogły być wyrównane łącznie w następnym etapie obliczeń, a wyrównanie można wykonać w państwowym układzie wysokości.

Etap 2
To będzie finalne, łączne wyrównanie hybrydowej sieci wysokościowej w państwowym układzie wysokości. Wykonamy go przechodząc w programie do zakładki SIEĆ 1D.
Do wyrównania potrzebne będą następujące pliki:
Stale1D.txt - plik wysokości punktów nawiązania sieci w państwowym układzie wysokości,
DeltaH.txt - przewyższenie niwelacji geometrycznej między punktami 1138 i 1071,
DeltaHb.txt - przewyższenia niwelacyjne pomiędzy reperami i ich ekscentrami GNSS,
DhGPS.txt - plik przewyższeń utworzony w etapie I, czyli plik przewyższeń normalnych odpowiadających pomierzonym wektorom GNSS.
W pliku DhGPS.txt możemy usunąć wszystkie przewyższenia związane z punktem 9000, ponieważ nie są one potrzebne do wyrównania zaplanowanej sieci wysokościowej.

Wyrównanie zostaje zrealizowane po wciśnięciu przycisku Wykonaj wyrównanie. Wcześniej należy zadeklarować na panelu programu błędy a'priori dla poszczególnych rodzajów obserwacji co jest potrzebne do właściwego zwagowania sieci.

Zobacz raport wyrównania - Wyrównanie1D

Przykład nr 7 - Wyrównanie niwelacji satelitarnej - wyrównanie 1D

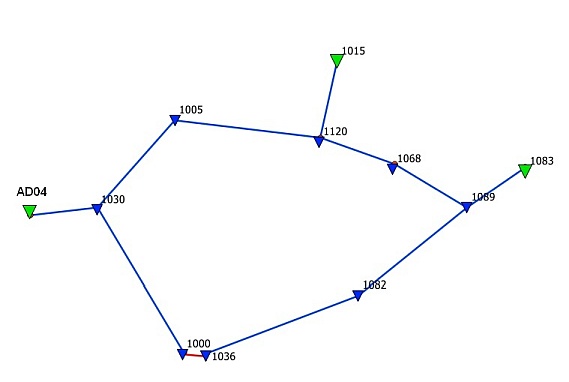
Wyznaczane jest tu 8 nowych reperów osnowy wysokościowej. Sieć jest nawiązana na 3 repery osnowy wyższej klasy.
Metodą niwelacji satelitarnej zostały pomierzone odcinki pokazane kolorem niebieskim. Jeden krótki odcinek (pomiędzy reperami wyznaczanymi) został pomierzony za pomocą klasycznej niwelacji geometrycznej (kolor czerwony). Odcinek pomierzony klasycznie stanowi jednocześnie dobrą kontrolę, ponieważ zamyka figurę - ewentualny błąd na którymś z pokazanych odcinków niwelacji musi objawić się w wyrównaniu dużymi poprawkami do obserwacji.
Ważną okolicznością jest to, że wśród reperów nowych i reperów nawiązania istnieją repery ścienne, a więc takie których nie można stacjonować odbiornikiem GNSS. W związku z tym w pobliżu reperów ściennych założono ekscentry posiadające dobre warunki GNSS. Pomiary GNSS wykonano właśnie na wspomnianych ekscentrach. Natomiast jednym stanowiskiem niwelatora określono różnicę wysokości pomiędzy reperem i jego ekscentrem i te przewyższenia będą również uczestniczyć w finalnym wyrównaniu sieci. Tak wiec sytuacja konstrukcyjna, powiedzmy w okolicy "czerwonego" odcinka pomierzonego klasycznie wygląda następująco

W ramach postprocessingu oprócz wektorów obliczono również metodą SPP (Single Point Positioning) współrzędne punktu 1005, które posłużą do umiejscowienia sieci GNSS w przestrzeni. Dokładność tak pozyskanych współrzędnych jest wystarczająca do przekształcenia wektorów w przewyższenia normalne niwelacji satelitarnej.

Opracowanie numeryczne takiego zadania realizujemy w dwóch krokach, załączony przykład zawiera dane do obu etapów:

Etap 1
Jest to niezbędny etap wstępny, gdzie jakby wyrównaniu podlegają wyłącznie obserwacje GNSS. W tym celu wybieramy w programie opcję SIEĆ 3D i możemy wykonać obliczenia pomierzonej sieci GNSS. Punkty ekscentryczne pokazano na rysunku kółeczkami.

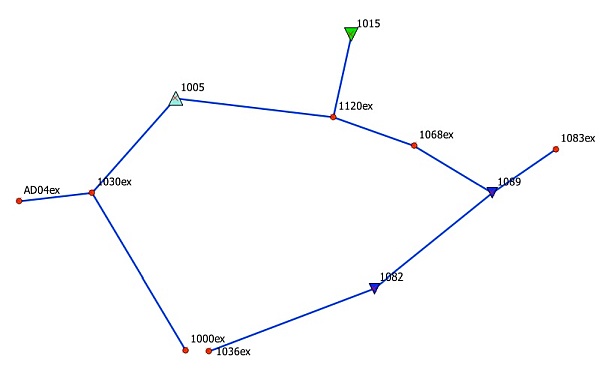
Wykonujemy tu wyrównanie pseudoswobodne w związku z tym jako punkt stały zostaje użyty wyżej wspomniany punkt 1005. Pozostałe punkty uzyskują współrzędne poprzez propagację dzięki czemu wszystkie wektory zostają umiejscowione w geocentrycznym układzie XYZ.
Na rysunku pokazano wektory stanowiące najistotniejsze odcinki niwelacji satelitarnej, które przyjęto do obliczeń. Nie ma przeszkód oczywiście, żeby dodawać do obliczeń również dodatkowe inne wektory jakie mogą powstać w przypadku, gdy sesje pomiarowe były by realizowane przez kilka odbiorników.

Do wyrównania wchodzą dwa pliki: - Wektory.txt oraz Stale3D.txt.
Najważniejszym efektem tego etapu obliczeń jest to, że po wyrównaniu program utworzy plik pn. DhGPS.txt, który zawiera przewyższenia ΔH odpowiadające pomierzonym wektorom. Istotne jest to, że są to przewyższenia normalne, a nie przewyższenia elipsoidalne. Tylko przewyższenia normalne są spójne co do rodzaju z przewyższeniami pochodzącymi z niwelacji geometrycznej, dzięki temu te dwa typy obserwacji będą mogły być wyrównane łącznie w następnym etapie obliczeń, a wyrównanie może być wykonane bezpośrednio w państwowym układzie wysokości.

Etap 2
To będzie finalne, łączne wyrównanie hybrydowej sieci wysokościowej w państwowym układzie wysokości. Wykonamy go przechodząc w programie do zakładki SIEĆ 1D.
Do wyrównania potrzebne będą następujące pliki:
- Stale1D.txt - plik wysokości punktów nawiązania sieci w państwowym układzie wysokości,
- DeltaH.txt - przewyższenie niwelacji geometrycznej między punktami 1000 i 1036,
- DeltaHb.txt - przewyższenia niwelacyjne pomiędzy reperami i ich ekscentrami GNSS,
- DhGPS.txt - plik przewyższeń utworzony w etapie I, czyli przewyższenia normalne odpowiadające pomierzonym wektorom GNSS.

Wyrównanie zostaje zrealizowane po wciśnięciu przycisku Wykonaj wyrównanie. Wcześniej należy zadeklarować na panelu programu błędy a'priori dla poszczególnych rodzajów obserwacji co jest potrzebne do właściwego zwagowania sieci.

Zobacz raport wyrównania - Wyrównanie1D

Przykład nr 8 - Wyrównanie niwelacji satelitarnej pomierzonej metodą RTN - wyrównanie 1D

Zadaniem jest tu numeryczne opracowanie niwelacji satelitarnej pomierzonej metodą RTN.

Chodziło o wyznaczenie wysokości dwóch punktów metodą niwelacji satelitarnej w nawiązaniu do dwóch reperów osnowy wysokościowej.
Pewnym utrudnieniem jest fakt, że reper nr 5011 jest reperem ściennym, a więc jest niedostępny do pomiaru GNSS.
Gdyby pomiary były realizowane metodą statyczną to szkic sieci dla takiego zadania wyglądałby jak obok. Przy reperze 5011 założono by ekscentr umożliwiający pomiar GNSS oraz pomierzono by geometrycznie przewyższenie pomiędzy tym ekscentrem i właściwym reperem.
Jednak pomiar satelitarny przeprowadzono tu jednym odbiornikiem metodą RTN co dość radykalnie zmienia organizację prac w terenie i szkic sieci. Natomiast nie zmienia to metodologii prac obliczeniowych związanych z wyrównaniem sieci - jest ona identyczna jak w przypadku metody statycznej.

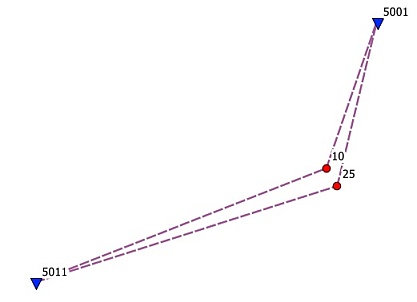
Szkic naprawdę zrealizowanej sieci przedstawia rysunek niżej. Obrazuje on następującą organizację prac w terenie.

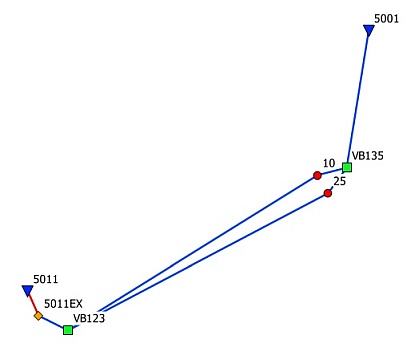
Wykonano inicjalizację odbiornika przy reperze 5011, odbiornik wygeneruje wirtualną stację bazową, którą oznaczono tu umownie VB123. Wykonujemy pomiar RTN na ekscentrze tego reperu a następnie przemieszczamy się na punkty nowo wyznaczane 10 i 25, które kolejno mierzymy. Ważne jest, że wszystkie te trzy punkty pomierzono przy zachowaniu tej samej wirtualnej stacji bazowej.
Następnie wykonujemy nową inicjalizację odbiornika, czyli zostaje wygenerowana wirtualna stacja bazowa VB135. Mierzymy ponownie punkty 10 i 25 a następnie reper 5001, który tym razem jest reperem ziemnym więc nie trzeba posiłkować się ekscentrem. Podobnie jak poprzednio wszystkie trzy punkty zostały pomierzone przy tej samej stacji bazowej.

Uzyskujemy w ten sposób 6 wektorów pokazanych na rysunku, które posłużą do wykonania niwelacji satelitarnej. Składowe dX, dY, dZ poszczególnych wektorów pobieramy z raportu pomiaru RTN. Z tego samego raportu pobieramy współrzędne wirtualnych stacji bazowych potrzebne w pierwszej fazie obliczeń do konwersji wektorów na przewyższenia normalne. Dobry raport pomiaru RTN powinien zawierać wszystkie te dane.Jeżeli dysponujemy plikiem odbiornikowym RW5 to potrzebny plik wektorów od stacji bazowych do punktów masówki obserwacyjnej oraz współrzędne tychże stacji bazowych możemy utworzyć (wyeksportować z RW5) za pomocą funkcji pomocniczej programu znajdującej się w zakładce Dodatki.

Jak widać z rysunku elementami tego układu są również punkty VB123 i VB135, które są jakby matematycznymi punktami pośrednimi w sieci, ale to nie przeszkadza.

Opracowanie numeryczne takiego zadania realizujemy w dwóch krokach, załączony przykład zawiera dane do obu etapów:

Etap 1
Jest to niezbędny etap wstępny, gdzie jakby wyrównaniu podlegają wyłącznie obserwacje GNSS. W tym celu wybieramy w programie opcję SIEĆ 3D i możemy wykonać obliczenia.

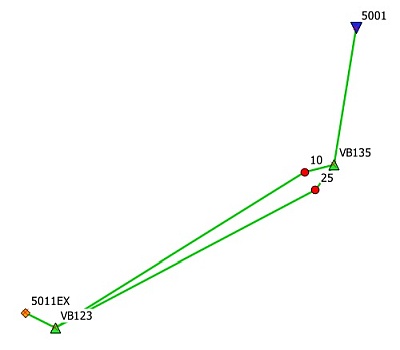
Do wyrównania wchodzą dwa pliki: Wektory.txt oraz Stale3D.txt.
W pliku punktów nawiązania umieszczamy współrzędne obu wirtualnych stacji bazowych, bo z raportu RTN (lub pliku RW5) mamy te dane. Ewentualnie możemy podać tu tylko jedną stację, wtedy otrzymamy wyrównanie pseudoswobodne.
Najważniejszym efektem tego etapu obliczeń jest to, że po wyrównaniu program utworzy plik pn. DhGPS.txt, który zawiera przewyższenia ΔH odpowiadające pomierzonym wektorom. Istotne jest to, że są to przewyższenia normalne, a nie przewyższenia elipsoidalne. Tylko przewyższenia normalne są spójne co do rodzaju z przewyższeniami pochodzącymi z niwelacji geometrycznej, dzięki temu te dwa typy obserwacji będą mogły być wyrównane łącznie w następnym etapie obliczeń.

Etap 2
To będzie finalne, łączne wyrównanie hybrydowej sieci wysokościowej w państwowym układzie wysokości. Wykonamy go przechodząc w programie do zakładki SIEĆ 1D. Sieć jest hybrydowa, ponieważ w skład obserwacji oprócz przewyższeń niwelacji satelitarnej musi wejść też przewyższenie klasyczne pomiędzy ekscentrem i rperem na punkcie 5011.
Do wyrównania potrzebne będą następujące pliki:
- Stale1D.txt - plik wysokości punktów nawiązania sieci w państwowym układzie wysokości,
- DeltaHb.txt - przewyższenia niwelacyjne pomiędzy reperem i ekscentrem GNSS,
- DhGPS.txt - plik przewyższeń utworzony w etapie I, czyli przewyższenia normalne odpowiadające pomierzonym wektorom GNSS.
Wyrównanie zostaje zrealizowane po wciśnięciu przycisku Wykonaj wyrównanie. Wcześniej należy zadeklarować na panelu programu błędy a'priori dla poszczególnych rodzajów obserwacji, co jest potrzebne do właściwego zwagowania sieci.

Zobacz raport wyrównania - Wyrównanie1D